Q.What is intelligence?

Real intelligence is what determines the normal thought process of a human. Artificial

intelligence is a property of machines which gives it ability to mimic the human thought process.

The intelligent machines are developed based on the intelligence of a subject, of a designer, of a person, of a human being.

Now two questions:

can we construct a control system that hypothesizes its own control law?

We encounter a plant and looking at the plant behavior, sometimes, we have to switch from one control system to another control system where the plant is operating. The plant is may be operating in a linear zone or nonlinear zone; probably an operator can take a very nice intelligent decision about it, but can a machine do it? Can a machine actually hypothesize a control law, looking at the model? Can we design a method that can estimate any signal embedded in a noise without assuming any signal or noise behavior?

That is the first part; before we model a system, we need to observe. That is we collect certain data from the system and How do we actually do this? At the lowest level, we have to sense the environment, like if I want to do temperature control I must have temperature sensor. This data is polluted or corrupted by noise.

How do we separate the actual data from the corrupted data?

This is the second question. The first question is that can a control system be able to hypothesize its own control law? These are very important questions that we should think of actually. Similarly, also to represent knowledge in a world model, the way we manipulate the objects in this world and the advanced is a very high level of intelligence that we still do not understand; the capacity to perceive and understand.

Q. What is AI ?

Artificial Intelligence is concerned with the design of intelligence in an artificial device. The term was coined by McCarthy in 1956. There are two ideas in the definition.

1. Intelligence 2. artificial device

Practical applications of AI

AI components are embedded in numerous devices e.g. in copy machines for automatic

correction of operation for copy quality improvement. AI systems are in everyday use for

identifying credit card fraud, for advising doctors, for recognizing speech and in helping

complex planning tasks. Then there are intelligent tutoring systems that provide students with personalized attention. Thus AI has increased understanding of the nature of intelligence and found many applications. It has helped in the understanding of human reasoning, and of the nature of intelligence. It has also helped us understand the complexity of modeling human reasoning.

What is soft computing?

An approach to computing which parallels the remarkable ability of the human mind to reason and learn in an environment of uncertainty and imprecision. It is characterized by the use of inexact solutions to computationally hard tasks such as the solution of nonparametric complex problems for which an exact solution can’t be derived in polynomial of time.

Why soft computing approach?

Mathematical model & analysis can be done for relatively simple systems. More complex

systems arising in biology, medicine and management systems remain intractable to

conventional mathematical and analytical methods. Soft computing deals with imprecision,

uncertainty, partial truth and approximation to achieve tractability, robustness and low solution cost. It extends its application to various disciplines of Engg. and science.

Typically human can:

1. Take decisions

2. Inference from previous situations experienced

3. Expertise in an area

4. Adapt to changing environment

5. Learn to do better

6. Social behaviour of collective intelligence

Intelligent control strategies have emerged from the above mentioned characteristics of human/ animals.

The first two characteristics have given rise to Fuzzy logic; 2nd , 3rd and 4th have led to Neural Networks; 4th , 5th and 6th have been used in evolutionary algorithms.

Characteristics of Neuro-Fuzzy & Soft Computing:

1. Human Expertise

2. Biologically inspired computing models

3. New Optimization Techniques

4. Numerical Computation

5. New Application domains

6. Model-free learning

7. Intensive computation

8. Fault tolerance

9. Goal driven characteristics

10. Real world applications

Intelligent Control Strategies (Components of Soft Computing):

The popular soft computing components in designing intelligent control theory are:

1. Fuzzy Logic

2. Neural Networks

3. Evolutionary Algorithms

Fuzzy logic: Most of the time, people are fascinated about fuzzy logic controller. At some point of time in Japan, the scientists designed fuzzy logic controller even for household appliances like a room heater or a washing machine. Its popularity is such that it has been applied to various engineering products.

Fuzzy number or fuzzy variable: We are discussing the concept of a fuzzy number. Let us take three statements: zero, almost zero, near zero. Zero is exactly zero with truth value assigned 1. If it is almost 0, then I can think that between minus 1 to 1, the values around 0 is 0, because this is almost 0. I am not very precise, but that is the way I use my day to day language in interpreting the real world. When I say near 0, maybe the bandwidth of the membership which represents actually the truth value. You can see that it is more, bandwidth increases near 0. This is the concept of fuzzy number.

Neural networks :

Neural networks are basically inspired by various way of observing the biological organism.

Most of the time, it is motivated from human way of learning. It is a learning theory. This is an artificial network that learns from example and because it is distributed in nature, fault tolerant, parallel processing of data and distributed structure.

The basic elements of artificial Neural Network are: input nodes, weights, activation function and output node. Inputs are associated with synaptic weights. They are all summed and passed through an activation function giving output y. In a way, output is summation of the signal multiplied with synaptic weight over many input channels.

Features of Artificial Neural Network (ANN) models:

1. Parallel Distributed information processing

2. High degree of connectivity between basic units

3. Connections are modifiable based on experience

4. Learning is a continuous unsupervised process

5. Learns based on local information

6. Performance degrades with less units

Soft Computing

Hard Computing

Soft Computing is liberal of inexactness,

uncertainty, partial truth and approximation.

Hard computing needs a exactly state analytic

model.

Soft Computing relies on formal logic and

probabilistic reasoning.

Hard computing relies on binary logic and

crisp system.

Soft computing has the features of

approximation and dispositionality.

Hard computing has the features of

exactitude(precision) and categoricity.

Soft computing is stochastic in nature.

Hard computing is deterministic in nature.

Soft computing works on ambiguous and noisy

data.

Hard computing works on exact data.

Soft computing can perform parallel

computations.

Hard computing performs sequential

computations.

Soft computing produces approximate results.

Hard computing produces precise results.

Soft computing will emerge its own programs.

Hard computing requires programs to be

written.

Soft computing incorporates randomness .

Hard computing is settled.

10.

Soft computing will use multivalued logic.

Hard computing uses two-valued logic

Key Differences Between Fuzzy Set and Crisp Set



A fuzzy set is determined by its indeterminate boundaries, there exists an uncertainty

about the set boundaries.



Fuzzy set elements are permitted to be partly accommodated by the set (exhibiting

gradual membership degrees).



There are several applications of the crisp and fuzzy set theory, but both are driven

towards the development of the...



The fuzzy set follows the infinite-valued logic whereas a crisp set is based on bi

valued logic.

********************************************************************

THEANO >>

Program 1:

import theano
import numpy as np
import theano.tensor as T
x=T.matrix()
y=T.vector()
b = theano.shared(np.random.uniform(-1,1),name="b")
W = theano.shared(np.random.uniform(-1.0, 1.0, (1, 2)), name="W")
print(W)
y=W.dot(x)+b
print(y)

Output:

W Elemwise{add,no_inplace}.0

Program2:

import tensorflow as tf

from theano import *

b=tf.Variable(tf.ones([1]))

print(b)

Output:

<tf.Variable 'Variable:0' shape=(1,) dtype=float32, numpy=array([1.], dtype=float32)>

Program 3:

from theano import *

a=tensor.dscalar()

b=tensor.dscalar()

c=a*b

f=theano.function([a,b],c)

d=f(12.5,4.5)

print(d)

Output:

56.25

Program 4:

import tensorflow

from theano import *

a=tensor.dmatrix()

b=tensor.dmatrix()

c=tensor.dot(a,b)

f=theano.function([a,b],c)

d = f([[0, -1, 2],[4, 11, 2]], [[3, -1],[1,2],[6,1]])

print(d)

theano.printing.pydotprint(f, outfile="sc.png", var_with_name_simple=True)

Output:

[[11. 0.] [35. 20.]]

Program 5:

#pitts model

#w1=1,w2=1,AND operation

import theano.tensor as T

from theano import *

from theano.ifelse import ifelse

import numpy as np

x=T.vector('x')

w=theano.shared(np.array([1,1]))

z=T.dot(x,w)

c=ifelse(T.lt(z,0),0,1)

f1=theano.function([x],c)

x = [

[0 ,0],

[0 ,1],

[1, 0],

[1 ,1]

]

for i in range(len(x)):

t=x[i]

op=f1(t)

print('output: x1=%d & x2=%d is %d' % (t[0],t[1],op))

Output:

output: x1=1 & x2=1 is 1

************************** ************************** **************************

Properties of Fuzzy Sets

Fuzzy sets are defined as sets that contain elements having varying degrees of membership values. Given A and B are two fuzzy sets, here are the main properties of those fuzzy sets:

Commutativity :-

(A ∪ B) = (B ∪ A)
(A ∩ B) = (B ∩ A)

Associativity :-

(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)

Distributivity :-

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Idempotent :-

A ∪ A = A
A ∩ A = A

Identity :-

A ∪ Φ = A => A ∪ X = X
A ∩ Φ = Φ => A ∩ X = A

Note: (1) Universal Set ‘X’ has elements with unity membership value.
(2) Null Set ‘Φ’ has all elements with zero membership value.

Transitivity :-

If A ⊆ B, B ⊆ C, then A ⊆ C

Involution :-

(A^c)^c = A

De morgan Property :-

(A ∪ B)^c = A^c ∩ B^c
(A ∩ B)^c = A^c ∪ B^c

Note: A ∪ A^c≠ X ; A ∩ A^c≠ Φ

Since fuzzy sets can overlap “law of excluded middle” and “law of contradiction” does not hold good.

************************************************************************

ASSOCIATIVE PROPERTY IN FUZZY SET

def UNION(A, B):
result = dict()
for A_key, B_key in zip(A, B):
    A_val = A[A_key]
    B_val = B[B_key]
    # Union
    if A_val > B_val:
      result[A_key]=A_val
    else:
      result[B_key]=B_val
return result

def check(A, B):
for A_key, B_key in zip(A, B):
    A_val = A[A_key]
    B_val = B[B_key]
    if A_val != B_val:
      return False
return True

A = dict()
B = dict()
C = dict()

A={"A1": 0.4,"A2": 0.7,"A3": 0.3,"A4": 0.6}
B={"B1": 0.5,"B2": 0.6,"B3": 0.6,"B4": 0.4}
C={"B1": 0.1,"B2": 0.8,"B3": 0.3,"B4": 0.6,}

Y1 = UNION(UNION(A, B), C)
Y2 = UNION(A, UNION(B, C))
print("=======Result===========")
print("Y1: ",Y1)
print("y2: ",Y2)
print(check(Y1, Y2))

Output:

Link: https://www.theprogrammingcodeswarehouse.com/2020/03/implementation-of-fuzzy-operations-on.html

******* ******* ******* ******* ******* ******* ******* ******* *******

MAPPING

f: X -> Y

y= f(x) = x^2

y = f(x), f is a mapping or function

f is also called formal method or an algorithm

***************************************************************************

Basics of Soft Computing

What is Soft Computing?

The idea of soft computing was initiated in 1981 when Lotfi A. Zadeh published his first

paper on soft data analysis “What is Soft Computing”.

Zadeh, defined Soft Computing into one multidisciplinary system as the fusion of the

fields of Fuzzy Logic, Neuro-Computing, Evolutionary and Genetic Computing, and

Probabilistic Computing.

Soft Computing is the fusion of methodologies designed to model and enable solutions to real world problems, which are not modeled or too difficult to model mathematically.

The aim of Soft Computing is to exploit the tolerance for imprecision, uncertainty,

approximate reasoning, and partial truth in order to achieve close resemblance with

human like decision making.

The Soft Computing – development history

SC = EC + NN + FL

Soft Computing = Evolutionary Computing + Neural Network + Fuzzy Logic

Zadeh 1981 = Rechenberg 1960 + McCulloch 1943+ Zadeh 1965

EC Evolutionary Computing Rechenberg 1960 = GP Genetic Programming Koza 1992 + ES Evolution Strategies Rechenberg 1965 + EP Evolutionary Programming Fogel 1962 + GA Genetic Algorithms Holland 1970

Definitions of Soft Computing (SC)

Lotfi A. Zadeh, 1992 : “Soft Computing is an emerging approach to computing which parallel the remarkable ability of the human mind to reason and learn in a environment of uncertainty and imprecision”.

The Soft Computing consists of several computing paradigms mainly :

Fuzzy Systems, Neural Networks, and Genetic Algorithms.

Fuzzy set : for knowledge representation via fuzzy If – Then rules.

Neural Networks : for learning and adaptation

Genetic Algorithms : for evolutionary computation

These methodologies form the core of SC.

Hybridization of these three creates a successful synergic effect; that is, hybridization creates a situation where different entities cooperate advantageously for a final outcome.

Soft Computing is still growing and developing.

Hence, a clear definite agreement on what comprises Soft Computing has not yet been reached.

More new sciences are still merging into Soft Computing.

Goals of Soft Computing

Soft Computing is a new multidisciplinary field, to construct new generation of

Artificial Intelligence, known as Computational Intelligence.

The main goal of Soft Computing is to develop intelligent machines to provide solutions

to real world problems, which are not modeled, or too difficult to model mathematically.

Its aim is to exploit the tolerance for Approximation, Uncertainty, Imprecision, and

Partial Truth in order to achieve close resemblance with human like decision making.

Approximation : here the model features are similar to the real ones, but not the same.

Uncertainty : here we are not sure that the features of the model are the same as that of the entity (belief).

Imprecision : here the model features (quantities) are not the same as that of the real

ones, but close to them.

Importance of Soft Computing

Soft computing differs from hard (conventional) computing. Unlike hard computing, the soft computing is tolerant of imprecision, uncertainty, partial truth, and approximation. The guiding principle of soft computing is to exploit these tolerance to achieve tractability, robustness and low solution cost. In effect, the role model for soft computing is the human mind.

The four fields that constitute Soft Computing (SC) are : Fuzzy Computing (FC), Evolutionary Computing (EC), Neural computing (NC), and Probabilistic Computing (PC), with the latter subsuming belief networks, chaos theory and parts of learning theory.

Soft computing is not a concoction, mixture,or combination, rather, Soft computing is a partnership in which each of the partners contributes a distinct methodology for addressing problems in its domain. In principal the constituent methodologies in Soft computing are complementary rather than competitive. Soft computing may be viewed as a foundation component for the emerging field of Conceptual Intelligence.

Fuzzy Computing

In the real world there exists much fuzzy knowledge, that is, knowledge which is vague, imprecise, uncertain, ambiguous, inexact, or probabilistic in nature. Human can use such information because the human thinking and reasoning frequently involve fuzzy information, possibly originating from inherently inexact human concepts and matching of similar rather then identical experiences.

The computing systems, based upon classical set theory and two-valued logic, can not answer to some questions, as human does, because they do not have completely true answers.

We want, the computing systems should not only give human like answers but also describe their reality levels. These levels need to be calculated using imprecision and the uncertainty of facts and rules that were applied.

Fuzzy Sets

Introduced by Lotfi Zadeh in 1965, the fuzzy set theory is an extension of classical set theory where elements have degrees of membership.

Classical Set Theory

Sets are defined by a simple statement describing whether an element having a certain property belongs to a particular set.

When set A is contained in an universal space X, then we can state explicitly whether each element x of space X "is or is not" an element of A.

Set A is well described by a function called characteristic function A. This function, defined on the universal space X, assumes : value 1 for those elements x that belong to set A, and value 0 for those elements x that do not belong to set A.

The notations used to express these mathematically are

:Χ→ [0,1]

A(x) = 1 , x is a member of A A(x)

= 0 , x is not a member of A

Eq.(1)

Alternatively, the set A can be represented for all elements x ∈ X by its characteristic function

A (x) defined as

1 if x ∈ X

A (x) =

otherwise

Thus, in classical set theory A (x) has only the values 0 ('false') and 1 ('true''). Such sets are called crisp sets.

Crisp and Non-crisp Set

As said before, in classical set theory, the characteristic function A(x) of Eq.(2) has only values 0 ('false') and 1 ('true'').

Such sets are crisp sets.

− For Non-crisp sets the characteristic function

A(x) can be defined.

The characteristic function A(x) of Eq. (2) for the crisp set is generalized for the Non-crisp sets.

This generalized characteristic function A(x) of Eq.(2) is called membership function.

Such Non-crisp sets are called Fuzzy Sets.

Crisp set theory is not capable of representing descriptions and classifications in many cases; In fact, Crisp set does not provide adequate representation for most cases.

The proposition of Fuzzy Sets are motivated by the need to capture and represent real world data with uncertainty due to imprecise measurement.

The uncertainties are also caused by vagueness in the language.

Example 1 : Heap Paradox

This example represents a situation where vagueness and uncertainty are inevitable.

If we remove one grain from a heap of grains, we will still have a heap.

However, if we keep removing one-by-one grain from a heap of grains, there will be

a time when we do not have a heap anymore.

The question is, at what time does the heap turn into a countable collection of grains

that do not form a heap? There is no one correct answer to this question.

Example 2 : Classify Students for a basketball team

This example explains the grade of truth value.

tall students qualify and not tall students do not qualify

if students 1.8 m tall are to be qualified, then

should we exclude a student who is 1 /10" less? or should we exclude a student who is 1" shorter?

Non-Crisp Representation to represent the notion of a tall person.

A student of height 1.79m would belong to both tall and not tall sets with a particular degree of membership. As the height increases the membership grade within the tall set would increase whilst the membership grade within the not-tall set would decrease.

Capturing Uncertainty

Instead of avoiding or ignoring uncertainty, Lotfi Zadeh introduced Fuzzy Set theory that captures uncertainty.

In the case of Crisp Sets the members of a set are : either out of the set, with membership of degree " 0", or in the set, with membership of degree " 1 ",

Therefore, Crisp Sets ⊆ Fuzzy Sets In other words, Crisp Sets are Special cases of Fuzzy Sets.

Example 2: Set of SMALL ( as non-crisp set) Example 1: Set of prime numbers ( a crisp set)

If we consider space X consisting of natural numbers ≤12

ie X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Then, the set of prime numbers could be described as follows.

PRIME = {x contained in X | x is a prime number} = {2, 3, 5, 6, 7, 11}

A Set X that consists of SMALL cannot be described;

for example 1 is a member of SMALL and 12 is not a member of SMALL.

Set A, as SMALL, has un-sharp boundaries, can be characterized by a function that assigns a real number from the closed interval from 0 to 1 to each element x in the set X.

Definition of Fuzzy Set

A fuzzy set A defined in the universal space X is a function defined in X which assumes values in the range [0, 1].

A fuzzy set A is written as a set of pairs {x, A(x)} as

A = {{x , A(x)}} , x in the set X

where x is an element of the universal space X, and A(x) is the value of the function A for this element.

The value A(x) is the membership grade of the element x in a fuzzy set A.

Example : Set SMALL in set X consisting of natural numbers ≤ to 12.

Assume:

SMALL(1) = 1, SMALL(2) = 1, SMALL(3) = 0.9, SMALL(4) = 0.6,

SMALL(5) = 0.4, SMALL(6) = 0.3, SMALL(7) = 0.2, SMALL(8)

= 0.1, SMALL(u) = 0 for u >= 9.

Then, following the notations described in the definition above :

Set SMALL = {{1, 1 }, {2, 1 }, {3, 0.9}, {4, 0.6}, {5, 0.4}, {6, 0.3}, {7, 0.2}, {8, 0.1}, {9, 0 }, {10, 0 }, {11, 0}, {12, 0}}

Note that a fuzzy set can be defined precisely by associating with each x , its grade of membership in SMALL.

Definition of Universal Space

Originally the universal space for fuzzy sets in fuzzy logic was defined only on the integers. Now, the universal space for fuzzy sets and fuzzy relations is defined with three numbers. The first two numbers specify the start and end of the universal space, and the third argument specifies the increment between elements. This gives the user more flexibility in choosing the universal space.

Example : The fuzzy set of numbers, defined in the universal space

X = { xi } = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} is presented as

SetOption [FuzzySet, UniversalSpace → {1, 12, 1}]

What is intelligence?

Real intelligence is what determines the normal thought process of a human.

Artificial intelligence is a property of machines which gives it ability to mimic the human

thought process. The intelligent machines are developed based on the intelligence of a

subject, of a designer, of a person, of a human being. Now two questions: can we construct a control system that hypothesizes its own control law? We encounter a plant and looking at the plant behavior, sometimes, we have to switch from one control system to another control system where the plant is operating. The plant is may be operating in a linear zone or non linear zone; probably an operator can take a very nice intelligent decision about it, but can a machine do it? Can a machine actually hypothesize a control law, looking at the model? Can we design a method that can estimate any signal embedded in a noise without assuming any signal or noise behavior?

That is the first part; before we model a system, we need to observe. That is we collect

certain data from the system and How do we actually do this? At the lowest level, we have to sense the environment, like if I want to do temperature control I must have temperature

sensor. This data is polluted or corrupted by noise. How do we separate the actual data from the corrupted data? This is the second question. The first question is that can a control system be able to hypothesize its own control law? These are very important questions that we should think of actually. Similarly, also to represent knowledge in a world model, the way we manipulate the objects in this world and the advanced is a very high level of intelligence that we still do not understand; the capacity to perceive and understand.

What is AI ?

Artificial Intelligence is concerned with the design of intelligence in an artificial device.

The term was coined by McCarthy in 1956.

There are two ideas in the definition.

artificial Intelligence

artificial device

What is intelligence?

– Is it that which characterize humans? Or is there an absolute standard of judgement?

– Accordingly there are two possibilities:

– A system with intelligence is expected to behave as intelligently as a human

– A system with intelligence is expected to behave in the best possible manner

– Secondly what type of behavior are we talking about?

– Are we looking at the thought process or reasoning ability of the system?

– Or are we only interested in the final manifestations of the system in terms of its

actions?

Given this scenario different interpretations have been used by different researchers as defining the scope and view of Artificial Intelligence.

One view is that artificial intelligence is about designing systems that are as intelligent as

humans. This view involves trying to understand human thought and an effort to build

machines that emulate the human thought process. This view is the cognitive science approach

to AI.

The second approach is best embodied by the concept of the Turing Test. Turing held that in

future computers can be programmed to acquire abilities rivaling human intelligence. As part

of his argument Turing put forward the idea of an 'imitation game', in which a human being

and a computer would be interrogated under conditions where the interrogator would not

know which was which, the communication being entirely by textual messages. Turing argued

that if the interrogator could not distinguish them by questioning, then it would be

unreasonable not to call the computer intelligent. Turing's 'imitation game' is now usually

called 'the Turing test' for intelligence.

Logic and laws of thought deals with studies of ideal or rational thought process and inference.

The emphasis in this case is on the inferencing mechanism, and its properties. That is how the

system arrives at a conclusion, or the reasoning behind its selection of actions is very

important in this point of view. The soundness and completeness of the inference mechanisms

are important here.

The fourth view of AI is that it is the study of rational agents. This view deals with building

machines that act rationally. The focus is on how the system acts and performs, and not so

much on the reasoning process. A rational agent is one that acts rationally, that is, is in the best possible manner.

Typical AI problems

While studying the typical range of tasks that we might expect an “intelligent entity” to perform,

we need to consider both “common-place” tasks as well as expert tasks.

Examples of common-place tasks include

– Recognizing people, objects.

– Communicating (through natural language).

– Navigating around obstacles on the streets

These tasks are done matter of factly and routinely by people and some other animals.

Expert tasks include:

Medical diagnosis.

Mathematical problem solving

Playing games like chess

These tasks cannot be done by all people, and can only be performed by skilled specialists.

Now, which of these tasks are easy and which ones are hard? Clearly tasks of the first type are easy for humans to perform, and almost all are able to master them. However, when we look at what computer systems have been able to achieve to date, we see that their achievements include performing sophisticated tasks like medical diagnosis, performing symbolic integration, proving theorems and playing chess.On the other hand it has proved to be very hard to make computer systems perform many routine tasks that all humans and a lot of animals can do. Examples of such tasks include navigating our way without running into things, catching prey and avoiding predators. Humans and animals are also capable of interpreting complex sensory information. We are able to recognize objects and people from the visual image that we receive. We are also able to perform complex social functions.

Intelligent behaviour

This discussion brings us back to the question of what constitutes intelligent behaviour. Some of these tasks and applications are:

Perception involving image recognition and computer vision

Reasoning

Learning

Understanding language involving natural language processing, speech processing

Solving problems

Robotics

Practical applications of AI

AI components are embedded in numerous devices e.g. in copy machines for automatic

correction of operation for copy quality improvement. AI systems are in everyday use for

identifying credit card fraud, for advising doctors, for recognizing speech and in helping complex planning tasks. Then there are intelligent tutoring systems that provide students with personalized attention.

Thus AI has increased understanding of the nature of intelligence and found many applications. It has helped in the understanding of human reasoning, and of the nature of intelligence. It has also helped us understand the complexity of modeling human reasoning.

Approaches to AI

Strong AI aims to build machines that can truly reason and solve problems. These machines

should be self aware and their overall intellectual ability needs to be indistinguishable from that

of a human being. Excessive optimism in the 1950s and 1960s concerning strong AI has given

way to an appreciation of the extreme difficulty of the problem. Strong AI maintains that suitably

programmed machines are capable of cognitive mental states.

Weak AI: deals with the creation of some form of computer-based artificial intelligence that

cannot truly reason and solve problems, but can act as if it were intelligent. Weak AI holds that

suitably programmed machines can simulate human cognition.

Applied AI: aims to produce commercially viable "smart" systems such as, for example, a

security system that is able to recognise the faces of people who are permitted to enter a

particular building. Applied AI has already enjoyed considerable success.

Cognitive AI: computers are used to test theories about how the human mind works--for example, theories about how we recognise faces and other objects, or about how we solve abstract problems.

Limits of AI Today

Today‟s successful AI systems operate in well-defined domains and employ narrow, specialized

knowledge. Common sense knowledge is needed to function in complex, open-ended worlds.

Such a system also needs to understand unconstrained natural language. However these

capabilities are not yet fully present in today‟s intelligent systems.

What can AI systems do

Today‟s AI systems have been able to achieve limited success in some of these tasks.

In Computer vision, the systems are capable of face recognition

In Robotics, we have been able to make vehicles that are mostly autonomous.

In Natural language processing, we have systems that are capable of simple machine

translation.

Today‟s Expert systems can carry out medical diagnosis in a narrow domain

Speech understanding systems are capable of recognizing several thousand words continuous speech

Planning and scheduling systems had been employed in scheduling experiments with

The Learning systems are capable of doing text categorization into about a 1000 topics

In Games, AI systems can play at the Grand Master level in chess (world champion), checkers,

etc.

What can AI systems NOT do yet?

Understand natural language robustly (e.g., read and understand articles in a newspaper)

Surf the web

Interpret an arbitrary visual scene

Learn a natural language

Construct plans in dynamic real-time domains

Exhibit true autonomy and intelligence

Applications:

We will now look at a few famous AI system that has been developed over the years.

1. ALVINN: Autonomous Land Vehicle In a Neural Network

In 1989, Dean Pomerleau at CMU created ALVINN. This is a system which learns to control

vehicles by watching a person drive. It contains a neural network whose input is a 30x32 unit two dimensional camera image. The output layer is a representation of the direction the

vehicle should travel.

The system drove a car from the East Coast of USA to the west coast, a total of about 2850

miles. Out of this about 50 miles were driven by a human, and the rest solely by the system.

2. Deep Blue

In 1997, the Deep Blue chess program created by IBM, beat the current world chess

champion, Gary Kasparov.

3. Machine translation

A system capable of translations between people speaking different languages will be a

remarkable achievement of enormous economic and cultural benefit. Machine translation is

one of the important fields of endeavour in AI. While some translating systems have been

developed, there is a lot of scope for improvement in translation quality.

4. Autonomous agents

In space exploration, robotic space probes autonomously monitor their surroundings, make

decisions and act to achieve their goals.

NASA's Mars rovers successfully completed their primary three-month missions in April,

2004. The Spirit rover had been exploring a range of Martian hills that took two months to

reach. It is finding curiously eroded rocks that may be new pieces to the puzzle of the region's past. Spirit's twin, Opportunity, had been examining exposed rock layers inside a crater.

5. Internet agents

The explosive growth of the internet has also led to growing interest in internet agents to

monitor users' tasks, seek needed information, and to learn which information is most useful.

What is soft computing?

An approach to computing which parallels the remarkable ability of the human mind to

reason and learn in an environment of uncertainty and imprecision.

It is characterized by the use of inexact solutions to computationally hard tasks such as the

solution of non parametric complex problems for which an exact solution can‟t be derived in

polynomial of time.

Why soft computing approach?

Mathematical model & analysis can be done for relatively simple systems. More complex

systems arising in biology, medicine and management systems remain intractable to

conventional mathematical and analytical methods. Soft computing deals with imprecision,

uncertainty, partial truth and approximation to achieve tractability, robustness and low

solution cost. It extends its application to various disciplines of Engg. and science. Typically

human can:

Take decisions

Inference from previous situations experienced

Expertise in an area

Adapt to changing environment

Learn to do better

Social behaviour of collective intelligence

Intelligent control strategies have emerged from the above mentioned characteristics of

human/ animals. The first two characteristics have given rise to Fuzzy logic;2nd , 3 rd and 4 th

have led to Neural Networks; 4th , 5th and 6th have been used in evolutionary algorithms.

Characteristics of Neuro-Fuzzy & Soft Computing:

Human Expertise

Biologically inspired computing models

New Optimization Techniques

Numerical Computation

New Application domains

Model-free learning

Intensive computation

Fault tolerance

Goal driven characteristics

Real world applications

Intelligent Control Strategies (Components of Soft Computing): The popular soft computing

components in designing intelligent control theory are:

Fuzzy Logic

Neural Networks

Evolutionary Algorithms

Fuzzy logic:

Most of the time, people are fascinated about fuzzy logic controller. At some point of time in

Japan, the scientists designed fuzzy logic controller even for household appliances like a

room heater or a washing machine. Its popularity is such that it has been applied to various

engineering products.

Fuzzy number or fuzzy variable:

We are discussing the concept of a fuzzy number. Let us take three statements: zero, almost zero, near zero. Zero is exactly zero with truth value assigned 1. If it is almost 0, then I can think that between minus 1 to 1, the values around 0 is 0, because this is almost 0. I am not very precise, but that is the way I use my day to day language in interpreting the real world. When I say near 0, maybe the bandwidth of the membership which represents actually the truth value.

You can see that it is more, bandwidth increases near 0. This is the concept of fuzzy number.

Without talking about membership now, but a notion is that I allow some small bandwidth when I say almost 0. When I say near 0 my bandwidth still further increases. In the case minus 2 to 2, when I encounter any data between minus 2 to 2, still I will consider them to be near 0. As I go away from 0 towards minus 2, the confidence level how near they are to 0 reduces; like if it is very near to 0, I am very certain. As I progressively go away from 0, the level of confidence also goes down, but still there is a tolerance limit. So when zero I am precise, I become imprecise when almost and I further become more imprecise in the third case.

When we say fuzzy logic, that is the variables that we encounter in physical devices, fuzzy numbers are used to describe these variables and using this methodology when a controller is designed, it is a fuzzy logic controller.

***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** ***** *****

HEURISTIC APPROACH

A heuristic technique, or a heuristic , is any approach to problem solving or self-discovery that employs a practical method that is not guaranteed to be optimal, perfect, or rational, but is nevertheless sufficient for reaching an immediate, short-term goal or approximation. Where finding an optimal solution is

impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution. Heuristics can be mental shortcuts that ease the cognitive load of making a decision. Examples that employ heuristics include using trial and error, a rule of thumb or an educated guess.

HEURISTIC APPROACH

TYPES OF HEURISTIC

Different types of heuristic models are:

❑ Representative Heuristic

❑ Availability Heuristic

❑ Anchoring Heuristic

❑ Sampling Heuristic

REPRESENTATIVE HEURISTIC

The representativeness heuristic involves estimating the likelihood of an event by comparing it to an existing prototype that already exists in our minds. ... When making decisions or judgments, we often use mental shortcuts or "rules of thumb" known as heuristics.

Example: Police suspecting a criminal according to crime

AVAILABILITY HEURISTIC

The availability heuristic, also known as availability bias, is a mental shortcut that relies on immediate examples that come to a given person's mind when evaluating a specific topic, concept, method or decision.

The availability heuristic operates on the notion that if something can be recalled, it must be important, or at least more important than alternative solutions which are not as readily recalled

SAMPLING HEURISTIC

heuristic sampling, is a generalization of Knuth’s original algorithm for estimating the efficiency of backtrack programs.

META HEURISTIC APPROACH

30In computer science and mathematical optimization, a meta heuristic is a higher-level procedure or heuristic designed to find, generate, or select a heuristic (partial search algorithm) that may provide a sufficiently good solution to an optimization problem, especially with incomplete or imperfect information or limited computation capacity. Meta heuristics

sample a subset of solutions which is otherwise too large to be completely enumerated or otherwise explored. Meta heuristics may make relatively few assumptions about the optimization problem being solved and so may be usable for a variety of problems.

MATPLOTLIB PYPLOT

PROGRAM 1:

import numpy as np
import matplotlib.pyplot as plt
a=np.array([12,24,45,27,36])
b=np.array([10,23,48,38,29])
#plt.plot(a)
#plt.plot(b)
plt.plot(a,b,color='r',marker='*',mec='g',mfc='pink',ms='15',linestyle='-.')

plt.title("A vs B")
plt.xlabel("1st array")
plt.ylabel("2nd array")
plt.grid(axis='y')
plt.bar(a,b)
plt.show()

PROGRAM 2:

import matplotlib.pyplot as plt
import numpy as np
x = np.random.normal(170, 10, 250)
plt.hist(x)
plt.show()

PROGRAM 3:

import numpy as np
import matplotlib.pyplot as plt
a=np.array([12,24,45,27,36])
b=np.array([10,23,48,38,29,89,47,89,76,65])
#plt.scatter(a,b)
plt.show()

PROGRAM 4:

import pandas as pd
import matplotlib.pyplot as plt
data={'age':[10,12,15,16,17,20,24,25,26,28,29,30],
'height':[4.8,4.9,4.8,5,5.1,5,5.2,5.4,5,5.1,5.2,5.3]}
df=pd DataFrame(data columns=['age' 'height'])
print(df)
plt.plot(df)
print(df.loc[1])
plt.show()

PROGRAM 5:

import matplotlib.pyplot as plt
import numpy as np
x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
colors = np.array(["red","green","blue","yellow","pink","black","orange","purple"])
plt.scatter(x, y, c=colors)
plt.show()

PROGRAM 6:

import matplotlib.pyplot as plt
import numpy as np
#day one, the age and speed of 13 cars:
x = np.array([5,7,8,7,2,17,2,9,4,11,12,9,6])
y = np.array([99,86,87,88,111,86,103,87,94,78,77,85,86])
plt.scatter(x, y)
#day two, the age and speed of 15 cars:
x = np.array([2,2,8,1,15,8,12,9,7,3,11,4,7,14,12])
y = np.array([100,105,84,105,90,99,90,95,94,100,79,112,91,80,85])
colors = np.array([0, 10, 20, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100])
plt.scatter(x, y,cmap='viridis',alpha=0.4)
plt.show()

PROGRAM 7:

import numpy as np
#plot 1:
x = np.array([0, 1, 2, 3])
y = np.array([3, 8, 1, 10])
#plt.plot(x,y)
plt.subplot(1,2,1)
plt.plot(x,y)

#plot 2:
x = np.array([0, 1, 2, 3])
y = np.array([10, 20, 30, 40])
plt.subplot(1, 2, 2)
plt.plot(x,y)
plt.show()

*******************************************************************************************

NUMPY MATPLOTLIB PYPLOT

PROGRAM 1:

import numpy as np
a=np.array([12,74,55,46,81])
a.sort()
print(a[::-1])

PROGRAM 2:

import numpy as np
r1=np.random.randint(20,60,(4,5))
print(r1)
np.hsplit(r1,(3,4))

PROGRAM 3:

import numpy as np
a=np.array([1,3,4,5,6])
x=a.copy()
a[0]=12
print(x)
print(a)

PROGRAM 4:

import numpy as np
a=np.array([1,3,4,5,6])
x=a.view()
a[0]=12
print(x)
print(a)

PROGRAM 5:

import numpy as np
import matplotlib.pyplot as plt
a=np.array([23,34,12,56])
#plt.plot(a)
b=np.array([34,45,15,24])
#plt.plot(b)
plt.plot(a,b,'*:r')
plt.title("x and y plotting")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()

*******************************************************************************************

PANDAS THEANO TENSOR IFELSE

PROGRAM 1:

import pandas as pd
d=[1,2,3,4,5,6]
df=pd.DataFrame(d)
df

PROGRAM 2:

import pandas as pd
d=pd.read_csv("/content/drive/MyDrive/Colab Notebooks/Iris.csv")
df=pd.DataFrame(d)
print(df)
print(df.loc[1])

PROGRAM 3:

import cv2
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
image=cv2.imread("/content/drive/MyDrive/cat.jpg")
h, w = image.shape[:2]
#extracting height and image of an image
print("Height = {}, Width = {}".format(h, w))

(B,G,R)=image[150,100]
#extracting RGB format of an image

print("R = {}, G = {}, B = {}".format(R, G, B))
roi = image[100 : 500, 200 : 700]
#resize image

center=(w // 2,h // 2)
matrix = cv2.getRotationMatrix2D(center, -45, 1.0)
# resize() function takes 2 parameters,
# the image and the dimensions

resize = cv2.resize(image, (800, 800))

imgplot = plt.imshow(image)

plt.show()

PROGRAM 4:

import pandas as pd
d=[1,2,3,5,7]
d1=pd.Series(d)
d1

PROGRAM 5:

import theano
import theano.tensor as T
from theano.ifelse import ifelse
x=T.vector('x')
w=T.vector('w')
b=T.scalar('b')
z=T.dot(x,w) +b
a = ifelse(T.lt(z,0),0,1)
A=theano.function([x,w,b],a)
ip=[
[0,0],
[0,1],
[1,0],
[1,1]]
weight=[1,1]
bias=-1.5
for i in range(len(ip)):
t=ip[i]
out=A(t,weight,bias)
print('The output for x1=%d & x2=%d is %d' % (t[0],t[1],out))

PROGRAM 6:

import theano
import theano.tensor as T
from theano.ifelse import ifelse
#Define variables:
x = T.vector('x') w = T.vector('w') b = T.scalar('b')
#Define mathematical expression:
z = T.dot(x,w) +b
a = ifelse(T.lt(z,0),0,1) A = theano.function([x,w,b],a)
#Define inputs and weights
ip = [[0, 0],
[0, 1],
[1, 0],
[1, 1] ]
weights = [ 1,-1]
bias = -2
#Iterate through all inputs and find outputs:
for i in range(len(ip)):
    t = ip[i]
    out = A(t,weights,bias)
    print ('The output for x1=%d & x2=%d is %d' % (t[0],t[1],out))

************************************************************************************

PANDAS 2

PROGRAM 1:

#pandas series - one column in a table

import pandas as pd
a=[1,3,5,7,9,10]
s=pd.Series(a)
s

PROGRAM 2:

#INDEX SERIES

import pandas as pd
h1 = {"person1":149, "person2":152, "person3":157, "person4":151}
hgt=pd.Series(h1)
print(h1)
print("print the series")
print(hgt)
print(hgt.dtypes)

PROGRAM 3:

#Pandas Data frame
import pandas as pd

d={"roll":["MCA001","MCA003","MCA005","MCA007","MCA0013","MCA0014",], "name":["Doctor","Rutual","John","Queen","Julet","Rings",]}

df=pd.DataFrame(d)

#print whole list
print("Print total list")
print(df)

print("print from the top of the list")
#print from the top
print(df.head(3))

print("print from a specific location:")
print(df.loc[0])

PROGRAM 4:

#read csv file using pandas
#step 1: first prepare the csv file
#step 2: If you are using google colab upload it to the colab notebook folder
#step 3: mount the drive from colab prompt, for this check left side of the ...
#step 4: Click on the three dots in the right side of the file.. copy the ....

#step 5: write the following code

#import pandas as pd
df= pd.read_csv("/content/drive/MyDrive/Colab Notebook/iris.csv")
df

PROGRAM 5:

#DATA FRAME CAN TAKE NUMPY ARRAY AS DATA
import numpy as np
import pandas as pd
n1= np.array([12,34,45,56,78],[23,72,56,67,60])
n2=pd.DataFrame(n1)
n2

PROGRAM 6:

import pandas as pd

#Define a dictionary containing Student data

data = {'Name':['Jai','Prince','Gaurab','Anuj'],
'Height': [5.1, 6.2, 5.1 , 5.2],
'Qualification':['Msc','MA','Msc','Msc']}

#Convert the dictionary into DataFrame
df = pd.DataFrame(data)

#Declare a list that is to be converted into a column
address=['Delhi','Bangalore','Chennai','Patna']

#Using 'Address' as the column name and equating it to the list
df['Address'] = address

#Observe the result
print(df)

#add new row in the dataframe
n1= pd.DataFrame({'Name':['Ravi'], 'Height':[5.4],
'Qualification':['MCA']}, index=[4])

df=pd.concat([n1,df]).reset_index(drop = True)

print("printing table after adding new row")
print(df)

**************************************************************************************************************

ADALINE

PROGRAM 1:

#AND-NOT gate using ADALINE NETWORK

x1=[1,1,-1,-1]
x2=[1,-1,1,-1]
t=[-1,1,-1,-1]

w1= 0.2
w2= 0.2
b = 0.2
a= 0.2
e= [0,0,0,0]
for j in range(15):
   sum=0;
   print("Epoch= ",j+1)
   for i in range(4):
        yin = b + x1[i] * w1 + x2[i] *w2
        d = t[i] - yin
        w1 = w1 + a*d *x1[i]
        w2 = w2 + a * d *x2[i]
        b= b+ a*d
        e[i] = d*d
        print("error = ",e)
        sum = sum +e[i]
   print("Mean error= ",sum)

*****************************************************************************

Adaline Neural Network

•Known as Adaptive Linear Neuron
•Adaline is a network with a single linear unit
•The Adaline network is trained using the delta rule
ADALINE (Adaptive Linear Neuron or later Adaptive Linear Element) is an early
single-layer artificial neural network and the name of the physical device that implemented this network

ADALINE (Adaptive Linear Neuron or later Adaptive Linear Element) is an early single-layer
artificial neural network and the name of the physical device that implemented this network
The network uses memistors. It was developed by Professor Bernard Widrow
and his graduate student Ted Hoff at Stanford University in 1960.
It is based on the McCulloch–Pitts neuron. It consists of a weight, a bias and a summation function.

Adaline is a single layer neural network with multiple nodes where each node accepts multiple inputs and generates one output. Given the following variables as:
x is the input vector
w is the weight vector
n is the number of input
Theta some constant
y is the output of the model
then we find that the output is y = Summation xj . wj + theta. If we further assume that

x0 = 1
w0 = theta

then the output further reduces to y = Summation xj . wj

As already stated Adaline is a single-unit neuron, which receives input from several units and also from one unit, called bias. An Adeline model consists of trainable weights. The inputs are of two values (+1 or -1) and the weights have signs (positive or negative).
Initially random weights are assigned. The net input calculated is applied to a quantizer transfer function (possibly activation function) that restores the output to +1 or -1. The Adaline model compares the actual output with the target output
and with the bias and the adjusts all the weights.

Training Algorithm
The Adaline network training algorithm is as follows:
Step0: weights and bias are to be set to some random values but not zero. Set the learning rate parameter α.
Step1: perform steps 2-6 when stopping condition is false.
Step2: perform steps 3-5 for each bipolar training pair s:t
Step3: set activations foe input units i=1 to n.
Step4: calculate the net input to the output unit.
Step5: update the weight and bias for i=1 to n
Step6: if the highest weight change that occurred during training is smaller than a specified tolerance then stop the training process, else continue. This is the test for the stopping condition of a network.

Testing Algorithm
It is very essential to perform the testing of a network that has been trained. When the training has been completed, the Adaline can be used to classify input patterns. A step function is used to test the performance of the network. The testing procedure for the Adaline network is as follows:
Step0: initialize the weights. (The weights are obtained from the training algorithm.)
Step1: perform steps 2-4 for each bipolar input vector x.
Step2: set the activations of the input units to x.
Step3: calculate the net input to the output units
Step4: apply the activation function over the net input calculated.

Madaline- Multilayer Adaptive Linear Neural Network
•Stands for multiple adaptive linear neuron
•It consists of many adalines in parallel with a single output unit whose value is based on certain selection rules.
•It uses the majority vote rule
•On using this rule, the output unit would have an answer either true or false.

•On the other hand, if AND rule is used, the output is true if and only if both the inputs are true and so on.
•The training process of madaline is similar to that of adaline

Architecture
It consists of “n” units of input layer and “m” units of adaline layer and “1” Unit of the Madaline layer Each neuron in the adaline and madaline layers has a bias of excitation “1” The Adaline layer is present between the input layer and the madaline layer; the adaline layer is considered as the hidden layer.

The main difference between the perceptron and the ADALINE is that the later
works by minimizing the mean squared error of the predictions of a linear function. This means that the learning procedure is based on the outcome of a linear function rather than on the outcome of a threshold function as in the perceptron

****************** ****************** ****************** ******************

Artificial Neural Network(ANN)

Introduction to Artificial Neural Network(ANN)
Module III:Artificial Neural Network

✔ The term "Artificial Neural Network" is derived from Biological neural networks that
develop the structure of a human brain.

✔ Similar to the human brain that has neurons interconnected to one another, artificial neural
networks also have neurons that are interconnected to one another in various layers of the
networks. These neurons are known as nodes.
The given figure illustrates the typical diagram of Biological Neural Network.

Basic Structure of Artificial Neural Network
The typical Artificial Neural Network looks something like the given figure.

Dendrites from Biological Neural Network
represent inputs in Artificial Neural Networks,
cell nucleus represents Nodes, synapse
represents Weights, and Axon represents
Output.

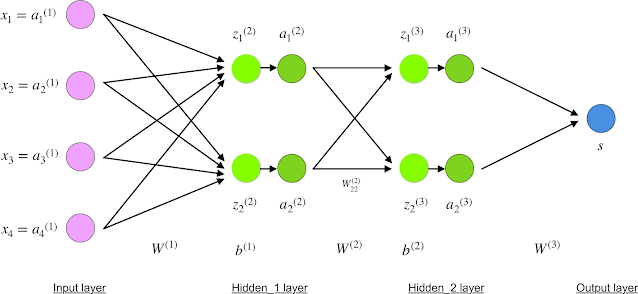
Architecture of Artificial neural network

✔ Artificial Neural Network primarily
consists of three layers:

Input Layer:
it accepts inputs in several different
formats provided by the programmer.

Hidden Layer:
The hidden layer presents in-between
input and output layers. It performs all
the calculations to find hidden features
and patterns.

Output Layer:
The input goes through a series of
transformations using the hidden layer,
which finally results in output that is
conveyed using this layer.

Architecture of Artificial neural network(Cont.)

✔ The artificial neural network takes input and computes the weighted sum of the inputs and
includes a bias. This computation is represented in the form of a transfer function.

✔ It determines weighted total is passed as an input to an activation function to produce the
output. Activation functions choose whether a node should fire or not. Only those who are
fired make it to the output layer. There are distinctive activation functions available that can
be applied upon the sort of task we are performing.

How do Artificial neural networks work

Feedforward Network

Feed forward Network:
✔ It is a non-recurrent network having processing Modules/nodes in layers and all the nodes
in a layer are connected with the nodes of the previous layers.
✔ Here is no feedback loop means the signal can only flow in one direction, from input to
output.
✔ It may be divided into the following two types :

Multilayer Feedforward Network

Multilayer feedforward network − The concept is of feedforward ANN having more
than one weighted layer. As this network has one or more layers between the input and
the output layer, it is called hidden layers.

Feedback Network

Feedback network:
✔ A feedback network has feedback paths, which means the signal can flow in both
directions using loops.
✔ This makes it a non-linear dynamic system, which changes continuously until it reaches a
state of equilibrium.
✔ It may be divided into the following types
Recurrent networks: They are feedback networks with closed loops.

Backpropagation Algorithm

Backpropagation algorithm is probably the most fundamental building block in a neural
network. It was first introduced in 1960s
The algorithm is used to effectively train a neural network through a method called
chain rule. In simple terms, after each forward pass through a network, backpropagation
performs a backward pass while adjusting the model’s parameters (weights and biases).

Backpropagation Algorithm

❑ Back propagation repeatedly adjusts the weights of the connections in the network so
as to minimize a measure of the difference between the actual output vector of the net
and the desired output vector.
❑ Compare the predicted output with input

Backpropagation Algorithm

Forward Propagation

Backpropagation Algorithm

Final Output

Feedback Network

Recurrent Neural Network

Following are the two types of recurrent networks:
Fully recurrent network − It is the simplest neural network architecture because all nodes
are connected to all other nodes and each node works as both input and output.

Jordan Network

Jordan network − It is a closed loop network in which the output will go to the input again
as feedback as shown in the following diagram. A Jordan Network is a Simple Recurrent
Network in which activations occur at the output layer, not at a hidden layer.

Advantages of Artificial Neural Network

Having fault tolerance
Having a memory distribution
Parallel processing capability
Storing data on the entire network

Disadvantages of Artificial Neural Network

Hardware dependence
Unknown duration
Difficulty of showing the issue of the network
Unrecognized behavior of the network

Frequently Asked Questions(FAQs)
1. What will happen to the network is no bias value is added in the network?
2. What is the role of cell nucleus in biological neural network? What will be
replaced by this, in case of ANN?
3. Design the architecture of artificial recurrent neural network model?
4. What are the advantages of back propagation algorithm?

Tabu Search is a commonly used meta-heuristic used for optimizing model parameters. A meta-heuristic is a general strategy that is used to guide and control actual heuristics. Tabu Search is often regarded as integrating memory structures into local search strategies. As local search has a lot of limitations, Tabu Search is designed to combat a lot of those issues.
The basic idea of Tabu Search is to penalize moves that take the solution into previously visited search spaces (also known as tabu).

Competitive learning is an unsupervised learning, where the nodes compete for responding to a subset of input data. It works by increase the specialization of each node in the network.

A= a1 0.6   a2 0.7   a3 0.5
B= b1 0.4   b2 0.7   b3 0.8

conjunction min value
0.4       0.7     0.5

negative
1-a
a1 0.4    a2 0.3     a3 0.5

1-b
b1   0.6    b2 0.3   b3 0.2

Conjunction is a truth-functional connective which forms a proposition out of two simpler propositions, for example, P and Q. The conjunction of P and Q is written P ∧ Q, and expresses that each are true

P={(0.3,0.5,0.7,0.8)     Q=     (0.5,0.8,0.9,1)

conjunction ={0.3 , 0.5, 0.7 ,0.8}
Negation = 1 - p
= {0.7 ,0.5 , 0.3 , 0.2 }
Disjuction = {0.5 , 0.8 , 0.9, 1}
impliction = {0.7, 0.3 , 0.2}

In fuzzy logic, the predicates can be fuzzy, for example, Tall, III, Young, Soon, MUCH Heavier, Friend of. Hence, we can have a (fuzzy) proposition like "Mary is Young." It is clear that most of the predicates in natural language are fuzzy rather than crisp

In classical logic, the only widely used predicate modifier is the negation NOT. In fuzzy logic, in addition to the negation modifier, there are a variety of predicate modifiers that act as hedges, for example, VERY, RATHER, MORE OR LESS, SLIGHTLY, A LITTLE, EXTREMELY. predicate modifiers are essential in generating the values of a linguistic variable. Here we can have a fuzzy proposition like "This house is EXTREMELY Expensive.

Fuzzy logic allows the use of fuzzy quantifiers exemplified by Most, Many, Several, Few, Much of, Frequently, Occasionally, About Five. Hence, we can have a fuzzy proposition like "Many students are happy." In fuzzy logic, a fuzzy quantifier is interpreted as a fuzzy number or a fuzzy proportion that provides an imprecise characterization of the cardinality of one or more fuzzy or nonfuzzy sets.

(John is Old) is NOT VERY True, in which the qualified proposition is (John is Old) and the qualifying fuzzy truth value is "NOT VERY True."

Today the temparature is very hot

hot predicate
very quantifier
proposition Partially false

Proposition values:
t(p) = 0.0 absolutely false
= 0.2 partially false
= 0.4 may be false
= 0.6 may be true
= 0.8 partially true
= 1.0 absolutely true

sham is very attentive in the class , this is not very true
= negative

what is fuzzy controller

A fuzzy control system is a control system based on fuzzy logic—a mathematical system that analyzes analog input values in terms of logical variables that take on continuous values between 0 and 1, in contrast to classical or digital logic, which operates on discrete values of either 1 or 0.

Differentiate between Fuzzy Set and Crisp Set

difference between hard computing and soft computing

Indicate biological analogies of the basic techniques of soft computing.

Does AI closely related to soft computing

Does AI is closely related to soft computing? Justify your answer

what are the difference of numpy array from traditional array
what are the advantage of numpy array over python list

is python object oriented?

Write a short note on transfer function or activation function

Explain Single Layer Feed-forward Network

Advantages and disadvantages of ANN

Deep learning

disadvantage of ANN

annonymous function in python

remove,del,pop

self organization map

how we can remove a blank space from a python string

what is fuzzy logic

what is single layer perceptron

purpose of perceptron learning

Regression analysis is a statistical method that helps us to analyze and understand the relationship between two or more variables of interest. The process that is adapted to perform regression analysis helps to understand which factors are important, which factors can be ignored, and how they are influencing each other.

RULES:
1. Information is stored in the connections between neurons in neural networks, in the form of weights.

2. Weight change between neurons is proportional to the product of activation values for neurons.

3. As learning takes place, simultaneous or repeated activation of weakly connected neurons incrementally changes the strength and pattern of weights, leading to stronger connections.

A decision boundary is the region of a problem space in which the output label of a classifier is ambiguous. If the decision surface is a hyperplane, then the classification problem is linear, and the classes are linearly separable . Decision boundaries are not always clear cut.

Search This Blog

SOFT COMPUTING

SC NOTES

THEANO >>

Properties of Fuzzy Sets

Commutativity :-

Associativity :-

Distributivity :-

Idempotent :-

Identity :-

Transitivity :-

Involution :-

De morgan Property :-

ASSOCIATIVE PROPERTY IN FUZZY SET

MAPPING

Artificial Neural Network(ANN)

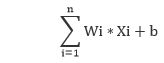
Comments

Post a Comment

Popular posts from this blog

SOFT COMPUTING MCQS

5 marks qus

Soft Computing Lab